印度音乐与西方音乐

译者：海瑞两千 原文地址：dhrupadmusic.com

印度音乐的心之所在就是拉格，拉格是一种调式（mood）、一种情调色彩（sentiment），通过微分音阶而得以表达。有许多不同的拉格，而每一种拉格都有其各自的调式以及与其自身相应的微分音程，它们都是建立在所谓自然泛音列——泛音自然排列的法则基础上的。

然而，在晚近100年左右的时间里，印度音乐却一直为外来的乐音体系所影响，而这外来的乐音体系并不是建立在自然泛音列的基础上的。这就是西方的乐音体系，它影响到印度音乐，主要是由于印度音乐家采用了有固定音高的西方乐器使然。簧风琴（harmonium），是这一状况中尤为突出的例子，在印度，如今它已是非常地流行了，且流布甚广。

  西方的乐音体系是建立在：将一个八度人为地分割为12个等距音程基础上的。这首先就意味着：所有的音实际上都跑调儿了，同时也表明：就音乐表达而言，与自然泛音列的无限可能性相比，其可资使用的音程数也是非常有限。

因此，使用基于西方乐音体系的、有着固定音高的乐器，若要正确地演奏拉格是不可能的。这就好像是：企图制作一幅绘画的副本，却没有与原作的原色相吻合。这样一种体系是根本无以表达自然音程的细微之处的，而大量拉格中所采用的正是自然音程。

然而，西方的乐音体系，如今不仅在世界上业已居于统治地位，在印度也是如此，这就使得拉格固有的微分音阶陷于迷失的危险。许多研究印度音乐的学者认为：这样发展下去是非常令人遗憾的，这不仅因为印度音乐是一种艺术形式，而且首要的是因为：拉格原本就是要用以培育唯识（ consciounsess）的一种方式。

由于原微分音阶为西方音阶的近似值所取代，拉格固有的力度和强度就会迷失——这不仅仅是出于理论上的考量，而且首先是基于经验的。有鉴于此，我们认为：提高对这个问题的意识是十分重要的。因此，我们对印度固有的乐音体系和西方的乐音体系做了如下的描述、比较和历史回顾。

音乐的本质

   音乐的本质，可谓：音际关系。只要我们在《牛津词典》里查阅一下“music”这个词，就会找到如下定义：

《牛津词典》“音乐（music）”的定义

以创造形式美、和谐美、以及情感表达美这样一种方式组合起来的人声或乐器（或：两者的组合）的声响。

无论是在西方的还是在印度的音乐传统中，乐音都排序为音阶，因此，音阶是音乐表达的基础。最常见的一种音阶有七个音，尽管它有时会少于七音，有时会多于七音。这种音阶中有一个音被称之为 主音（key note又译：基音、基调），是该音阶的基础音（basic note ）。假如可以把这个音阶比作一个家族的话，基音即如其母，而其余各音即如其子女。尽管有时子女们自己彼此间玩兴（playing）正酣，但却总有其母背后相随，而且终要回归母亲的怀抱。因此，音阶中诸音之间最重要的关系，是每一个音同其 主音之间的关系。

主音，就是我们由其开始构建一列音阶的那个起始音。音阶上的各音，往往是根据它们距离主音（基音）的位置来命名的。因此，音阶上的第二个音叫作“2音”；第四个音叫作“4音”；第五个音叫作“5音”，余类推。

纯律的音程

声音的本性

只要我们拨动吉他上的一根琴弦，它就会发出一个声音。这声音是由于振动中的琴弦使其周边空气中的分子发生振动而产生的。这振动在空间的所有方向上扩散，犹如池塘中的涟漪。当振动触动到我们的耳膜，耳膜亦随之振动，继而转化为神经脉冲，于是，我们便感知成一个有着一定音高的持续音。

空气以与弦同样的速度振动，而音高是由振动的速度决定的，这个振动速度即被称之为：频率。频率以赫兹（Hz：每秒钟振动的次数）为单位实施测量。琴弦振动的频率，取决于弦的长度、粗细度以及密度。

如果忽略潜在的增幅装置不计，振幅的大小决定着音量的大小。弦振动多久，频率、从而音高也就持续多久，与此同时，振幅会渐渐缩小，因而声音也就会慢慢消失。

泛音列的音程

   我们在听一根吉他琴弦发出的声音的时候，我们并不只是听到了一个音，而是多个不同音高的音。实际上，我们听到的是一个多个声音复合的结果。我们听到一个音，是因为其最显著，此即基础音，而其余的，则是所谓的泛音。音程，即这些声音之间在音高上的差异，并不是任意的，而是非常精确和有序的。

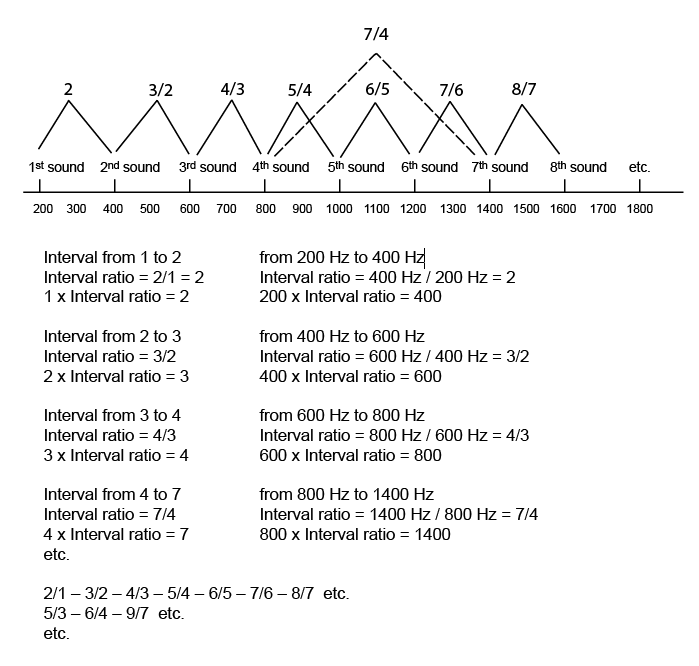
   除却琴弦物理介质可能有的限制性因素不论，泛音即是基础音频率的精确倍增。举例来说：如果主要声束（main sound ）的频率为200赫兹，那么第一个泛音，即 2音，为400赫兹，两倍于基频（ basic frequency）。第二泛音，或曰3音，为600赫兹，三倍于基频。第三泛音，或曰4音，为800赫兹，四倍于基频。第四泛音，或曰5音，为1000赫兹，五倍于基频，余类推。我们可以用下面这张以赫兹为单位的频率比例图来加以说明：

音及其泛音

 

    这个声音的序列就叫做”泛音列“，代表着一组自然音程的集合。它们体现的是声音之间自然的音差，亦称纯律的音程。在世界历史上几个最卓越的文化中，人们正是在这样的音程上构建各自的音阶的。在欧洲——整个中世纪乃至文艺复兴——也曾有这样一个普遍的共识：纯律的音程是音乐当然的基础。

纯律的音程可以表示为：泛音列的音数之比，即一个数除以另一个数。我们可通过如下方式对此做举例说明：

纯律的数学运算

sound=“音” Interval from to n = “从n 至 n 的音程” Interval ratio =“音程比” Hz=赫兹 泛音列中两个音之间的音程比即：后一音的音数除以前一音的音数。前一个音的音数乘以音程比，即可得到后一音的音数。兹说明如下： 我们的第一个音程是从1音至2音，此种情形即意谓：200赫兹至400赫兹。这亦称之为一个倍频程（octave：一个八度）。这个音程的比率即为2/1。由1乘以音程比，我们即得到2。如前述，200赫兹乘以音程比，得400赫兹，即2音的频率。 我们得到的第二个音程是从2音至3音，此种情形即是从400赫兹到600赫兹。这个音程的比率为：3/2。2乘以这个比值，得3。如前，400赫兹乘以这个比值，得600赫兹，即第3音的频率。 第三个音程，是从3音至4音，此种情形即是从600赫兹到800赫兹。这个音程的比率为4/3。3乘以这个音程比，即得4。如前，600赫兹乘以音程比，得800赫兹，即第4音的频率。 然而，也有由一个以上间隔构成的音程，例如：从4音至7，此种情形即是从800赫兹至1400赫兹。其音程比率为7/4。4乘以该音程比，即得7。如前，800赫兹乘以该音程比，得1400赫兹，即第7音的频率，如此等等。

构建自然音阶——纯律的音阶

从泛音列上可以找到所有不同大小、不同范围的音程。一个音程，或曰两个音程间的差别，可以小到非经训练的耳朵几乎无法听辨的程度。这样一种细小的差别即谓：微分音，因此，以泛音列为基础的音阶叫做微分音阶。

我们也可以这样看：其间涵有一数学架构。泛音列上所有的音程比率都是用整数来表达的。因此，自然音程，或曰纯律的音程，其特征所在就是：它们可以表示为整数比。这也是古希腊人（如：毕达哥拉斯）、苏美尔人、古代印度人、中国人以及世界历史上其他许多文化的发现，所有人都做如此想：音阶当以这样的音程为基础。

因此，可以选择一个基音来构建一个自然音阶，或曰纯律上的音阶，采用整数比音程相加的办法。选择哪些音程（间隔）以建构音阶，本身就是一门科学。依印度传统，音阶的音程间隔的选择是这样：直接演奏音符来创建某一特定的调式（mood ）或曰情调色彩（sentiment），此即所谓拉格。其间也有一个起码的原则，即：相对于数值较大的音数的音程比率而言，数值较小的音数的音程比率则更和谐，或曰协和。比率的数值变得越大，音程的协和度就变得越小，甚至不协和。

通过应用整数比，就可以在一个八度内创制一个音程集合，从最小的渐次进阶至较大的。于是这些音程便构成一个音列，人们可以从中选择数音用于一个音阶。

在欧洲的传统中，人们长久以往使用的是一种一个八度内有十二个音程的乐音体系，由叫做半音的乐音组成一个序列。人们从中选择数音用于各不相同的音阶。起初，西方音乐的这十二个音曾是依纯律的。

举例来说，我们可以优先考虑选择那些最协和的音程间隔，即有着最小音数比的音程，从而创建一个12音的集合，使这12个音稍微均匀些地分布在一个八度内。这样，我们就会有一个纯律的半音音列。我们可以从西方音乐中的标准音A开始，其频率为440赫兹。

纯律音列举隅

音名	频率	与起始音A的比率	与前一音的比率
1音	A	440.0000 Hz
2音	A#	469.3333 Hz	16/15	16/15	= 1.0667
2音	B	495.0000 Hz	9/8	135/128	= 1.0547
3音	C	528.0000 Hz	6/5	16/15	= 1.0667
3音	C#	550.0000 Hz	5/4	25/24	= 1.0417
4音	D	586.6667 Hz	4/3	16/15	= 1.0667
D#	616.0000 Hz	7/5	21/20	= 1.0500
5音	E	660.0000 Hz	3/2	15/14	= 1.0714
6音	F	704.0000 Hz	8/5	16/15	= 1.0667
6音	F#	733.3333 Hz	5/3	25/24	= 1.0417
7音	G	770.0000 Hz	7/4	21/20	= 1.0500
7音	G#	825.0000 Hz	15/8	15/14	= 1.0714
8度音	A	880.0000 Hz	2/1	16/15	= 1.0667
Hz=赫兹

 

如表所示，不妨计算一下半音之间的音程比。如是，须取得某一音的音程比——即计算其与主音（ key note ）之比；然后减去前一音的音程比——也是计算其与主音的比率。继而，用一音程比乘以欲减去的音程比的倒数。例如，欲找到A#与B的音程比，须从9/8这个音程比中减去16/15这个音程比，其乘法运算如 下：

 9/8 x 15/16 = 135/128。

也可以对音程比做加法计算。如是，须用一个比率乘以另外一个。例如：若对A至A#间的半音，其比率为16/15，与A#至B间的半音，其比率为135/128做加法计算，须作如 下计算：

16/15 x 135/128 = 9/8。

有关纯律调音的问题

从这十二个音的音列中，人们多半是选取七个音来构成一个音阶——通常是一序列的全音和半音。然而，在计算这十二个音音列中半音间的音程比时，我们发现：它们并非是等值的。A与A#之比是16/15，而A#与B之比却是135/128，诸如此类等等。这就意味：若要用不同的音与作为主音的A相比，这个序列的各音程就不会是相同的。这在实践上就意味着：若要将纯律应用于所谓固定音高的乐器，如风琴或钢琴，就必须使这类乐器基于某个具体的主音（key note）。要想改变主音，即意味：从另一不同音高的音重新开始同样的音阶，遂最有可能做的就是：不得不对整个乐器重新调律。

 由于人们想要时时都能够变换主音，甚至在乐曲的中途变换主音，当使用有固定音高的乐器的时候，这就成了西方音乐中的一个实际问题。我们不妨用下面这个例子来说明这个问题：

上面这个12音序列，是建立在A这个主音基础上的。如是，如果我们用这来构建A大调音阶，我们就会看到：假如我们把主音转换到C上，将会发生怎样的情形。A大调音阶由A – B – C# – D – E – F# – G#诸音构成，而C大调诸音则为：C – D – E – F – G – A – B。

纯律上的A大调音阶转为C大调音阶

音名	与A的比率	A大调音阶各音	与前一音的比率	C大调音阶各音	与前一音的比率
A	1音	A
A#	16/15
B	9/8	2音	B	9/8
C	6/5	1st	C
C#	5/4	3音	C#	10/9
D	4/3	4音	D	16/15	2nd	D	10/9
D#	7/5
E	3/2	5音	E	9/8	3rd	E	135/128
F	8/5	4th	F	16/15
F#	5/3	6音	F#	10/9
G	7/4	5th	G	35/32
G#	15/8	7音	G#	9/8
A	2/1	8度音	A	16/15	6th	A	8/7
B b	16/15
B	9/8	7th	B	9/8
C	6/5	Octave	C	16/15

我们看到：两个音阶各音之间的音程，在多数情况下趋于不同。例如：A大调的1音和2音之间，即A至B，其音程比率为9/8；而C音阶1音和2音之间，即C至D之间，其音程比率却是10/9。A大调音阶的2音和3音之间的音程比是10/9，而C音阶上的2音和3音的音程比却是135/128，如此等等。由于这两个音阶各音的音程，在多数情况下是不同的，故它们实际上是两个不同的音阶。因此，依这样的音程序列，若要将大调音阶的主音由A转至C，是不可能。

十二平均律体系

  因了这纯律调音中遇到的难题，在欧洲，多是在文艺复兴时期，人们便开始着手进行所谓调律（tempered tuning）的各种不同类型的实验，即：不断地修改纯律中的各音程，使之能够无须重新调音即可转换音阶的主音（转调）。历经多年，提出过许多各种各样的律制（systems of tempering ），终于，大约在1850年，被称作十二平均律的这个最简单化、最激进的律制成了标准，而且从那时起在西方音乐中一直沿袭至今。

      平均律使一个八度内十二个音之间的音程比均化，并且固定了各音的频率。例如，把钢琴键盘中间A音的频率设定为440赫兹。既然如此，我们不妨从这个频率开始，来计算一下平均律各半音间的音程比：

十二平均律各半音间频率比的计算方法

R=频率比
起始频率x R x R x R ……（12次）=起始频率x2

起始频率 x R 12 =起始 频率x2
(440 Hz x R 12 = 440 Hz x 2 = 880 Hz) 
1 x R12 = 2 
(440 Hz x R12 = 880 Hz) 
R = 12 √2 ≈ 1.0594630943593 
R 是一个无理数，不能换算为整数比。

A音的440赫兹乘以频比（R），可得下一半音的频率。然后，将这一新的频率乘以同样的比值，可得其后相邻半音的频率，诸如此类。如是，总共须乘12次，直至A的八度音，即钢琴键盘上下一个A音，为前一个A音的倍频。

   在这个公式中，可以用1来表示440Hz，用2来表示倍频。然后可以计算频率比为：1.0594630943593.。这是个无理数，表明其不能换算为整数比，同时也表明：其并不是一个与自然泛音列相一致的音程比。

  因此，为简洁起见。440Hz，即A音，乘以比值1.05946，得下一个半音的频率：466.1624 Hz，即A#音。这后一频率同样乘以比值：1.05946，得其后的频率为：493.8824 Hz，即B音，余类推。如是做12次之后，便达至八度音，即起始音的倍频。这就是十二平均律乐音体系。

       这个乐音体系采取的是一种折中的办法，即把各音程的谐振（consonance：和音）或曰和声（harmony），尽可能调和得在演奏任一调的音阶时，一个与另一个听起来一样协和。然而，这也就是说：除八度外，没有一个音程是与纯律的自然泛音列相一致的。为便于将这两个律制做一比较，我们可创制一张表格，把早先纯律的12音同与之相应的平均律的12音放在一起来加以对照：

十二平均律与纯律十二音的比较

音名	平均律的频率	纯律的频率	频差	与前一音之比
均	纯
1音	A	440.0000 Hz	440.0000 Hz	0.0000 Hz
2音	A#	466.1624 Hz	469.3333 Hz	-3.1709 Hz	1.05946	1.0667
2音	B	493.8824 Hz	495.0000 Hz	-1.1176 Hz	1.05946	1.0547
3音	C	523.2524 Hz	528.0000 Hz	-4.7476 Hz	1.05946	1.0667
3音	C#	550.0000 Hz	554.3648 Hz	+4.3648 Hz	1.05946	1.0417
4音	D	587.3296 Hz	586.6667 Hz	+0.6629 Hz	1.05946	1.0667
D#	622.2524 Hz	616.0000 Hz	+6.2524 Hz	1.05946	1.0500
5音	E	659.2564 Hz	660.0000 Hz	-0.7436 Hz	1.05946	1.0714
6音	F	698.4560 Hz	704.0000 Hz	-5.5440 Hz	1.05946	1.0667
6音	F#	739.9876 Hz	733.3333 Hz	+6.6543 Hz	1.05946	1.0417
7音	G	783.9920 Hz	770.0000 Hz	+13.9920 Hz	1.05946	1.0500
7音	G#	830.6100 Hz	825.0000 Hz	+5.6100 Hz	1.05946	1.0714
8度	A	880.0000 Hz	880.0000 Hz	0.0000 Hz	1.05946	1.0667

 

如表所示，纯律与平均律之间在频率上的差异也许看起来不大。因此，十二平均律的拥护者或许会说：这点差异没什么大不了的。他们也许会问：为什么纯律的音程就该是更可取的呢，就算它们是所谓自然的、与自然泛音是一致的又如何？

 要回答这个问题，我们先须仔细考量十二平均律体系的局限，而后将其对听者心灵的影响与纯律作一比较。

十二平均律体系的局限

十二平均律体系对音乐表达有着很大的局限。在纯律中，有效的音程数极大，而在十二平均律体系中，可资使用的音程却只有12个固定的。

世界上大部分地区的民间音乐和现当代音乐事实上也没有以这种形式存在，正好就说明了这一局限。但凡有人还只能被“自然音阶（the tempered scales）”绑架着，我们就不难看清这一点。这涉及到许多音乐风格（genres ），如：爱尔兰和英国的民间音乐、黑人灵歌（Negro Spirituals）、布鲁斯（Blues）、灵魂乐（Soul）、多数类型的爵士和摇滚。理由是：这些音乐流派严重依附于平均律律制中的那些对它们甚至并不是那么合用的音程，例如所谓的蓝调（blue notes），常常是把音阶中的第Ⅲ、第Ⅴ、第Ⅶ级音降低，但却又未降至到平均律中那个与之相邻的半音同样的高度。这些特殊的音符表现在这些风格音乐中的方方面面，是它们的生命血脉。没有这些特殊音符，它们就会失去各自的活力和魅人的能量。

在钢琴上营造某种令人错觉是蓝调的蓝调，如：非常快速地演奏半音音程；使某音处于两个半音之间的某个位置从而打造一种蓝调印象，这都是有可能实现的。因此，有的钢琴家凭藉他们的技能可以在一定程度上弥补平均律的局限。但这绝不等同于演奏蓝调本身——在平均律钢琴上是不可能做到的。

 对于印度音乐来说，平均律的局限性，显现得就更多了。印度如今大约有150种微分音阶，或曰拉格，其使用的音程要比平均律中的多得多的多，远不止那12个。

 至于固定音高的乐器，则又是一种局限：拉格演奏上的一个重要特色就是：在音阶的诸音间滑动。这在像钢琴、簧风琴这样固定音高乐器上是不可能的事情，因此，它们并不大适合用作独奏乐器来演奏印度的古典音乐，即使是对它们做了适当的调音。

此外，平均律的局限还在于：各音都是固定在各自确定的频率上。在印度传统音乐中，人们从不这样做。声音的每一个频率，都有其独具个性的影响力、独具个性的音质或给人以独具个性的感觉。如果没有这些与不同的声音频率相连接的不同的感觉，就如没有着点以指空弹不同的音调。十二平均律由于其固定了各音的频率，因而也就摈弃了许多频率——把它们从大自然的调色板中开除了。如果把声音千变万化的频率比作一幅色彩千差万别的色谱的话，这就好像是：画家只有其中很小量的设定好的有限色数用来作画。

音程对心灵的影响

与音程有关的另一非常须要重视的方面是：它们如何打动人心。印度有关音乐的经典文本，与毕达哥拉斯、柏拉图的希腊哲学一样，也主张有着正面效应的音乐，其关键因子是：它应当是愉悦心灵的。诸多研究显示，当人们听了纯律的各音程之后发现：与平均律中等值的音程相比，它们会更令人愉悦、感觉更美。实际上，人们却常常被搞糊涂了：当他们听过纯律中相应的音程之后再听平均律中的音程，便以为平均律各音程才是协和的或和谐的。

平均律于欧洲推行的时候，种种审美上的因由，也是其遭反对的主要理据。当时的音乐理论家觉得：平均律消减了每个和弦的纯度和音乐的审美诉求。

还有一点值得玩味的是，凡西方声名显赫的古典乐派的作曲家，没有一个为平均律写作过，包括：巴赫、莫扎特、贝多芬、舒伯特、舒曼、肖邦、李斯特、瓦格纳、勃拉姆斯、柴可夫斯基。甚至有人引用莫扎特的话说：谁要是用平均律来演奏他的音乐他就杀了谁。

然而，就平均律各音与纯律中相应之各音间频率上的差别而言，其差别并不是很大，这从各百分比可见，那为什么其各音程听起来会有这种舒服度上的差别呢？难道这会是鉴赏力的问题？或者某种安慰剂效应（placebo effect）？

协和与不协和

   这一问题的答案是：纯律各音程比平均律中相应的音程，要更协和，或曰更和谐，现代科学实验也可以证明这一点。

 协和（consonance ）一词，源于拉丁文：com（“与……一起”）+sonare（“声响”）。如果我们在维基百科中检索这个词，就会是如下的定义：